Draw a general line

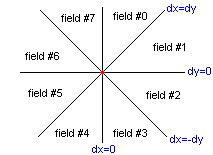
In the previous lesson we saw how to draw horizontal or vertical lines. These lines were special, because we only had to go straight horizontally or vertically. Therefore the steps between two pixels were well known, in the horizontal case it was 1, while for the vertical line it was 320 (one scanline). If we want to draw a general line in any direction, we have to do much more calculations. We know that the screen is buily by square pixels, but the points for a general line won't fit to these discrete places. So we have to approach the ideal line as much as we can.

On the following picture the red point in the center shows the start point of a general line. Whatever happens, on a 2D plane there are eight different fields based on the difference of dx and dy, where

  dx := x2 - x1   
  dy := y2 - y1

  (x1,y1) is the start point of the line
  (x2,y2) is the end point of the line

If dx is zero, we draw a vertical line. If dy is zero, we draw a horizontal line. If dx=dy or dx=-dy, it's a 45 degrees line. In any other case the line is totally general.

Have a look at the case when dx<dy. In this example dx=4 and dy=8. Becasue the smallest step on the screen is one pixel, for this line we have to increment the Y, and "sometimes" we have to increment the X. "Sometimes" is not a magic word, there is an exact calcualation form for finding out, when we have to increment the X. It is dy/dx, so in every second step we increment the X as well.
The theory is the same for the case dy<dx. Now we increment the X by one pixel, while the Y is incremented "sometimes". The number of pixels we have to draw is dx if dx>dy and dy if dy>dx. Based on the expression dx>dy we will have two different loops: "X incremental" or "Y incremental" loop.
Obviously, the dx/dy or dy/dx value most likely will not be an integer number! Anyway, we must try to reach the normal distribution for the pixels. The following picture shows a general line.

Now go down for one particular step, when one pixel follows the previous one. Whaever direction we have to move, in this small area there is only eight different place where we can go. For example the red arrow shows a step (-1,-1) while the blue arrow shows the step (0,-1).
In the implementation we are going to use a predefined array for these steps. This will be called Ntab and it will store the different values for moving the given direction. Something like this:
CaseNext StepNext Address
0(-1,-1)-321
1(0,-1)-320
2(1,-1)-319
7(-1,0)-1
3(1,0)+1
6(-1,1)+319
5(0,1)+320
4(1,1)+321

The array Ntab has 12 elements instead of 9, this because it's easier to handle in assembly. The value sgn(X) and sgn(Y) (sign function , -1 0 or 1) tell us which direction to go. 

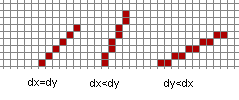
{ line steps for the 8 different directions }
const
   Ntab : array[0..11] of integer=(-321,-320,-319,000,
                                   -001, 000, 001,000,
                                    319, 320, 321,000);
var
   r1,r2,r3,r4,r5 : word; { some space to store temporary data }

procedure Line(x1,y1,x2,y2,color:integer); assembler;
asm
   mov  ES,SegA000     { Screensegment }

   mov  ax,320         { Address calculation }
   mul  y1
   add  ax,x1
   mov  di,ax

   mov  al,Color.byte
   mov  ES:[di],al     { We show the first pixel }

   mov  bx,0101h       { sgn X (BL), sgn Y (BH), both +1 }

   mov  dx,X2
   sub  dx,X1          { DX = X2-X1 }
   jnc  @t1
   neg  dx             { DX = abs X  (where X=X2-X1) }
   mov  bl,255         { BL = sgn X }
@t1:
   mov  si,Y2
   sub  si,Y1          { SI = Y2-Y1 }
   jnc  @t2
   neg  si             { SI = abs Y  (where Y=Y2-Y1) }
   mov  bh,255         { BH = sgn Y }
@t2:
   mov  cx,si          { CX = abs Y }
   mov  r2,bx          { r2 = sgn X sgn Y, we store them }

   cmp  dx,si          { what's the main direction? (X/Y) }
   jnc  @x_ge_y
   mov  r1,dx          { r1 = abs X }
   xor  bl,bl          { sgn X = 0 , X incremental line }
   jmp  @t3

@x_ge_y:
   test dx,dx          { abs X=abs Y=0 (it's only a pixel ) }
   jz   @exit
   mov  r1,si          { r1 = abs Y }
   mov  cx,dx          { cx = abs X }
   xor  bh,bh          { sgn Y = 0 , Y incremental line }
@t3:
   mov  r3,cx          { CX: number of pixels to draw }

   mov  ax,cx
   shr  ax,1           { AX = INT(CX/2) }

   { this main loop draws the line }

@line_loop:
   add  ax,r1          { increment }
   jc   @diag          { diagonal step }
   cmp  ax,r3
   jc   @vhl           { vertical or horizontal step }

@diag:                 { diagonal step }
   sub  ax,r3
   mov  r4,ax          { save AX  }
   mov  ax,r2          { orignal sgn X, sgn Y }
   jmp  @nextplot      { go to draw }

@vhl:                  { vertical or horizontal step }
   mov  r4,ax          { save AX  }
   mov  ax,bx          { computed sgn X and sgn Y  }

@nextplot:             { draw the pixel }
   mov  r5,bx          { save BX  }

   inc  al
   shl  al,1           { AL = (sgn X+1)*2, can be 0,2 or 4  }
   inc  ah
   shl  ah,3           { AH = (sgn Y+1)*8, can be 0,8 or 16 }
   add  al,ah
   xor  ah,ah
   lea  bx,Ntab        { BX points to the right element of Ntab }
   add  bx,ax
   add  di,[bx]        { so we make one step to the given direction }
   mov  al,Color.byte
   mov  ES:[di],al     { put the pixel }

   mov  ax,r4          { saved values back }
   mov  bx,r5
   loop @line_loop     { do the next step }
@exit:
end;

Do you understand? Well, I do not. :-) Yes, it's true, once I implemented, it was so clear for me, but right now it's just a mess. So don't be disappointed if you don't get it. Just use it.

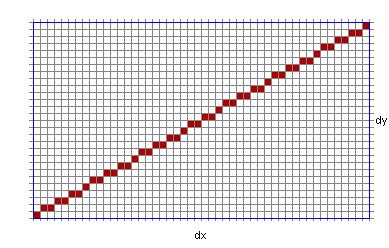
Test the result 

program lines;

uses gfx256;

var i : integer;

begin
 graph320x200;

 for i:=0 to 299 do
  line(random(320),random(200), random(320),random(200),random(256));

 readln;
 text80x25;
end.
This is what we see on the screen:

Downloads: [ Gfx256 unit | Lines ]

Back